There are times, we want to collaborate with other stakeholders in Github in a private manner. Meaning, we need to work and collaborate on a private Github repository. If you have a private Github private repository ready for collaboration, the most proven way to work with that is to leverage one of the following two options.
- Leverage SSH keys at the Github account level. So that you can work with Github private repository using SSH keys. The whole idea is that you will be generating an RSA key pair using SSH Key gen utility, add the private key portion of the key pair to the SSH agent and upload the public key portion of the key pair to the Github account settings. The advantage of this approach is that you have one SSH key defined at the Github account level to manage or work with all the private Github repositories created under that account.
- Leverage Deploy Keys at the individual repository level. I have learnt that a Deploy Key can be associated with only one Github repository at this point in time.

The advantage of the second approach is that you can have a dedicated key or set of deploy keys for individual repositories.
In this post, i’ll be covering the option #1. Basically i will leverage bash on windows 10 to work with private github repository using SSH keys. My windows 10 is already set up with Ubuntu 18.0.4 for Windows sub-system for linux. I’m not covering the steps for setting up bash on Windows 10 using Windows subsystem for linux. You can refer microsoft documenation for that. Let’s move to the SSH set up process for Github.
Navigate to the directory in windows 10, where you want to generate SSH key pair.

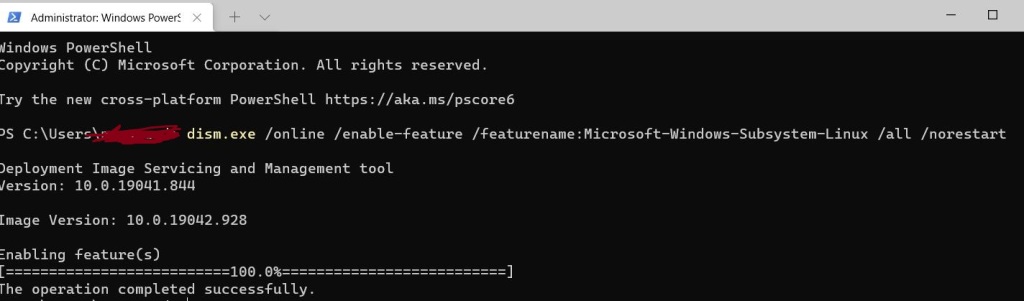
Type ‘bash’ on the command prompt. It will launch the bash shell on windows 10. Basically the Windows folder that you have pointed will be mounted to the ubuntu 18.0.4 bash shell.
Now you can generate the SSH key pair using ‘ssh-keygen’ utility.
ssh-keygen -t rsa -b 4096 -C “your_email@example.com“
Enter the name of the file for saving the key pair and provide any arbitrary passphrase when prompted.

Start the ssh on the bash shell. We need to explicty start it, because the run levels of this is different from a standard ubuntu desktop OS. I have learnt that the SSH agent does not get started automatically when you invoke bash on windows 10, unlike a standard ubuntu desktop OS.
eval $(ssh-agent -s)

Add the private key portion of the generated key pair to the SSH agent.
ssh-add keyname
If you getting a permission error for the generated key pair, the key will not get added successfully to the agent.

Even if you try to modify the permission of the key using ‘chmod 400’ or ‘chmod 600’ on the mounted directory, it won’t be successful. Becuase i’ve learnt that changing file permissions using chmod on the mounted directory (from windows 10) does not work.
The best way to fix this is to copy the key to a folder under the ubuntu user root directory, not to any windows mounted directory on bash.
Check if the directory ~/.ssh already exists on the bash shell. If not, explicitly create a directory ~/.ssh and exit the bash shell.
Again, navigate to the directory in windows 10 where the key pairs are generated and launch bash from there.
copy private key to ~/.ssh

Navigate to ~/.ssh and change permissions using any one of the following commands.
chmod 400 sundargitsshkey
chmod 600 sundargitsshkey

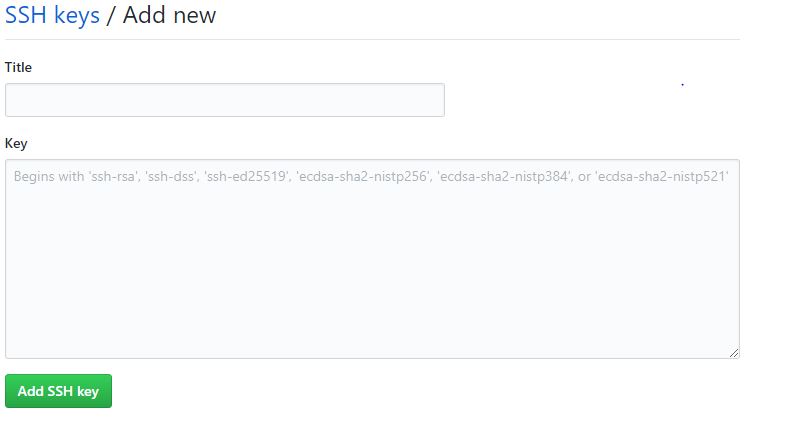
Copy the public key of the generated key pair (with ‘.pub’ suffix) to New –> SSH Key under Github account settings. Basically copy the content of the public key using any of the text editors and paste there in textbox available in New –> SSH Key under Github account settings.
Navigate to the SSH config file located in ‘/etc/ssh/ssh_config’ and add an entry for ‘IdentityFile ~/.ssh/sundargitsshkey’
sudo nano ssh_config

Start the SSH agent explicitly.
eval $(ssh-agent -s)
Verify the connectivity to Github using this command ‘SSH -T git@github.com’. You need to user the Github user name as ‘git’. If you try to use your actual Github user name, you’ll get errors.
It will ask you to confirm to accept the warning on authenticity of github.com. Accept it and provide passphrase for private key file when prompted. You’ll get the confirmation for successful authentication to make SSH calls into Github account from your bash shell.

Now you do git clone, commit and push to any number of repositories under your Github account using SSH, be it a private repository or public repository. This completes the post on working with Github private repository using bash on Windows 10.

























You must be logged in to post a comment.